When we think of beauty, we may recall a painting, a landscape, architecture, or Super Bowl XLII. Most of us place Math low on that list—but why?
Math was hard for me.
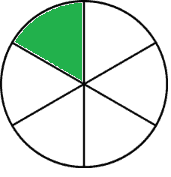
The first disconnect happened to me in fourth grade, during the fractions unit. I remember clearly that I was focused on “balancing” the top number on the tiny bar held up by the bottom number, then these cool shapes were placed on our table, and these cool shapes had cool names like “one half” and “one sixth.”
Don’t they mean “one-six”? These are funny names.
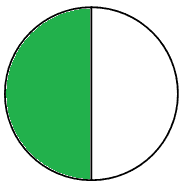
The next day, my teacher Mrs. B put up three of the one-sixth pieces (“should be one-six,” said my fourth-grade brain) and asked the class what it looks like. My classmate called out, “one half.”
“Correct.”
What? Three one-sixths can’t have two names!
I was so stuck in this vortex of confusion and insecurity that when the worksheet was handed out, we had to find the fractions’ second names and sometimes their third names, and I just couldn’t do it. It was the first time that I could remember not being able to do a whole page of math. Thankfully, my teacher had just enough time to help me out one-on-one for a few minutes, and finally I started to understand what was going on. She helped me reason that fractions are parts of a whole, and a whole can be broken apart in many ways.
Some of my teachers in later years had the time to help me out like Mrs. B did, but more than one could not find the time. Around the end of middle school, my love of discovering mathematics fizzled to a dull and dim struggle of just remembering the formulas enough to pass the next test.
I was no longer learning—I was doing anything to get an A and moving on.
I finally saw Math’s beauty in a high school geometry classroom.
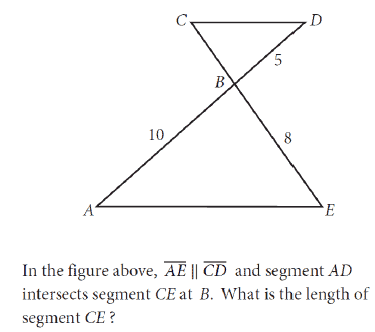
I was really worried about my first day in geometry. My previous year was the most I had struggled in math, and I just felt discouraged with the new school year. Mr. B started off the class by asking us to go into groups of four. He put up a problem like this question:
…and asked us to solve it.
What? It’s the first day!
Ten minutes of brain storming later, he asked each group how we got our answers. Not just “what is your answer”, nor did he discourage us from our long and drawn out explanations. He quietly nodded his head, wrote our theory on the white board, and listened to the next group. After hearing all of us, he then asked the class, “Which way makes the most sense?”

We couldn’t decide. Two groups had the same answer, so we were split between the two. He replied, “There are often multiple ways to get to the right answer in Math.” Then we cracked open our textbooks: he would explain the textbook’s way and alternate ways as well. We repeated this method of teaching every day for the rest of the school year. It was beautiful: many ways to be right, and, as long as I did correct operations, I would always get to the correct answer.
I was no longer asked to just remember a formula. I was given the chance to discover it myself.
My confidence in Math returned, to the point that I decided to major in Mathematics in college. I had started to research more Math topics on my own as well: Ada Lovelace and her brilliant calculator, Emmy Noether and her work with abstract Algebra, and the mystical Hypatia, who not only contributed to the STEM community but was also an icon for women’s rights.
I highly recommend discovering Math for yourself as well.
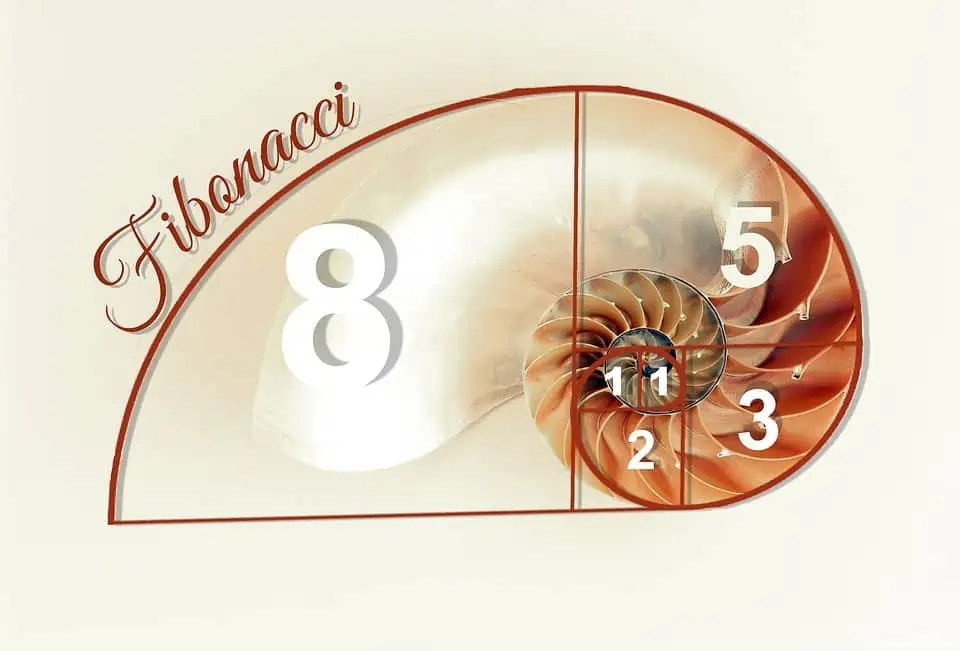
For example, the Fibonacci sequence looks like a mess of numbers, but it happens so naturally in life.

We can use the beauty of Math to solve for standard Math questions as well. For instance, trying to find the sum of interior angles in a sixteen-sided polygon:
Doing so can be intimidating, not only because we are dealing with angles, a shape, and a large number, but also because we are given seemingly foreign vocabulary. Our brain wants to shut down, guess, move on, anything to not do this problem.
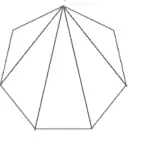
However, just like the pattern in a sunflower, Math can be solved by recognizing patterns. For example, we can build a pentagon (5 sides) using 3 triangles. We can build a hexagon (6 sides) with 4 triangles and a heptagon (7 sides) with 5 triangles.
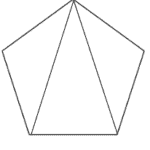
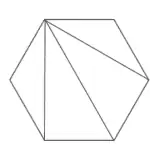
Following the pattern, a 16-sided polygon needs 14 triangles to build it. Each triangle has a sum of 180 degrees; therefore, 14 triangles multiplied by 180 degrees is 2,520 degrees. We do not even need to remember the formula to solve for the sum of the interior angles of a polygon if we can reason our way to the answer.
You can solve complicated problems by breaking them apart.
I followed my problem-solving methods through to graduation. These large and seemingly intimidating problems not only became palatable, but workable and fun! No longer was I stressed about not knowing the method – I saw these questions as puzzles, and most of the time my exploration led me to the correct answer. I took this discovery to heart and teach it to my students. I strive to inspire that same love, comfort, and appreciation of the beauty for Math in my students as well.
As writer Henry Miller says, “One’s destination is never a place but rather a new way of looking at things.” Take a breath, explore the problem, and discover the beauty of Mathematics.