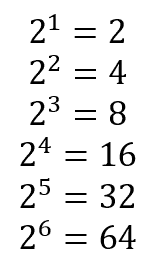Even if most Math taught in school seems useless, knowing this Math can help you make (lots of) money.
Students often feel that what they learn in school is not useful. For the most part, as we detailed here, that is an incorrect assumption, or at least simply speculation (because neither they nor anyone else can know with certainty whether what they learn will later be useful to them). Sometimes, even if students do not realize it, what they learned is extremely valuable. Consider the powers of two:
Pretty boring, right? Yes, unless you understand how that simple math can dramatically change your life and, often, the lives of your children, grandchildren, and their children. Here’s how.
Caution: the following will involve a small amount of Math (no surprise), but the payoff is worth it.
The Rule of 72
In investing, a simple trick to find a rough estimate of how long it will take your money to double is to divide 72 by your annual rate of return: it is appropriately called “The Rule of 72.” For example, suppose you invest $1,000 and get an average rate of 8% return per year, then (72 ÷ 8) = 9. It will take roughly 9 
years for your $1,000 to double and become $2,000.
By any standard, assuming a 7% annual rate of return on investments in a broad based, low-cost index fund (such as Vanguard’s or a competitor’s total stock market index fund) is a reasonable and likely conservative estimate. Conveniently, a 7% return also makes for easy math with the “Rule of 72”: (72 ÷ 7) ≈ 10. Thus, on average, you can expect that every 10 years your money will double if it is reasonably invested.
Powers of Two + Rule of 72
Combine the powers of two with the “Rule of 72,” and we have an incredibly powerful tool for understanding the importance and power of investing. Let’s explore.
To figure out how many times your money will double until retirement, for example, take your age of retirement (let’s say 65) and subtract your current age (let’s say 25, for this example): (65 − 25) = 40. That’s 40 years until retirement. If your money doubles every 10 years, then in 40 years it will have doubled 4 times. But, doubling 4 times gets you 16 times your original value. Let’s say “P” is your principal, or initial, investment. (P) × 2 × 2 × 2 × 2 = 16 × (P). Or, written with the powers of two: (P) × 24 = 16 × (P). Thus, any money you invest at age 25 will grow to 16 times its original value by retirement; put another way, $1,000 invested at age 25 will become $16,000. All you have to do is invest it and do nothing else.
Or, for example, just $1,000 invested for you by your parents when you were born will become $64,000 by the time you are 60 years old and $256,000 by the time you are 80 years old, which you could pass on to your children and that money would keep doubling every 10 years: $512,000 ⇒ $1,024,000 ⇒ $2,048,000 ⇒ etc. And it all started with only… $1,000.
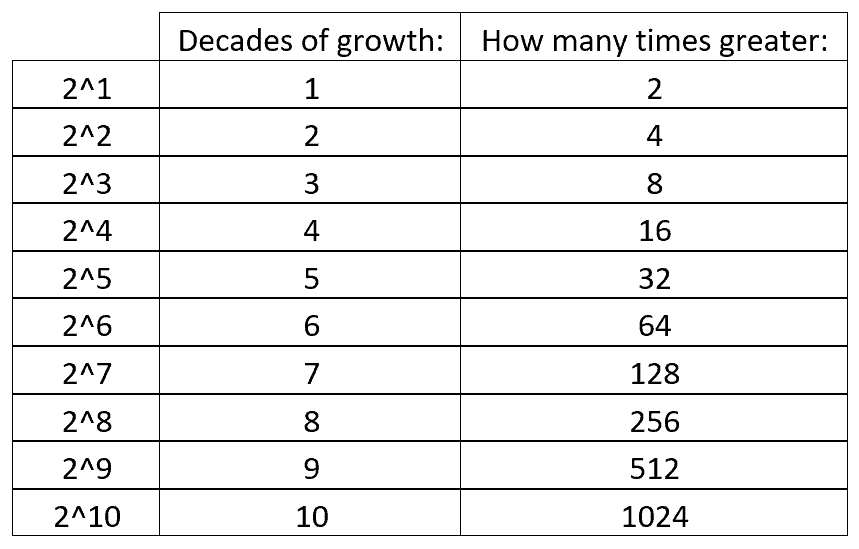
Thus, to calculate how much money your initial investment will have grown to, just multiply your initial money by 2 raised to the power of how many decades your money will grow for: (your initial investment) × 2(# of decades of growth) = (your ending investment balance). Below is a chart that simplifies how much to multiply your original investment by to figure out how much money you will have at the end of those decades and how many times greater your ending balance will be compared to your initial investment:
The Simple Math Behind a Massive Advantage
Knowledge helps us make better decisions. When we think about the long-term value of invested money, we can make better decisions about how to use money, both for our benefit and for that of others. A few exponents, a little division, and some multiplication can help us understand how to make life changing financial decisions.
hard-work + knowledge + time + compounding interest ⇒ generational wealth
